[Deep Learning] Chapter9. Convolutional Networks
Chapter 9. Convolutional Networks
9.1. The histroy of NN(Neural Network), CNN(Convolutinoal Neural Network)
(추후 추가 예정)
9.2. Convolutional Layer
Fully Connected Layer(이하 FC)를 사용하여 이미지를 처리하는 경우를 살펴보겠습니다. 32x32x3 사이즈의 이미지가 있을때(3은 RGB chanel입니다.) 이를 길게 늘려서 3072x1형태의 matrix로 만듭니다. 그리고 이를 10x3072 size의 weights와 내적하여 10x1크기의 activation matrix를 도출하게 됩니다. 이런식의 이미지 처리방식은 이미지의 공간적 구조를 보존하지 못한다는 단점이 있습니다.
Convolutional Layer(이하 conv)는 이미지의 공간적 구조를 보존한다는 특징이 있습니다. 32x32x3 size의 image가 input으로 주어졌을 때, 5x5x3 filter를 사용하여 합성곱 연산을 수행합니다. 필터를 가지고 이미지를 슬라이딩 하면서 공간적으로 내적을 수행하게 됩니다. filter의 depth인 3은 image의 depth와 같게되어 activation maps는 28x28x1 size가 됩니다. filter의 개수만큼 새로운 activation map을 도출할 수 있습니다. 각 필터를 가지고 전체 이미지에 convolution 연산을 수행한다고 요약할 수 있습니다. 이런식으로 간단한 linear layer로 된 nural network를 만들 수 있습니다. 그림1에서 해당 과정을 시각적으로 나타내고 있습니다.
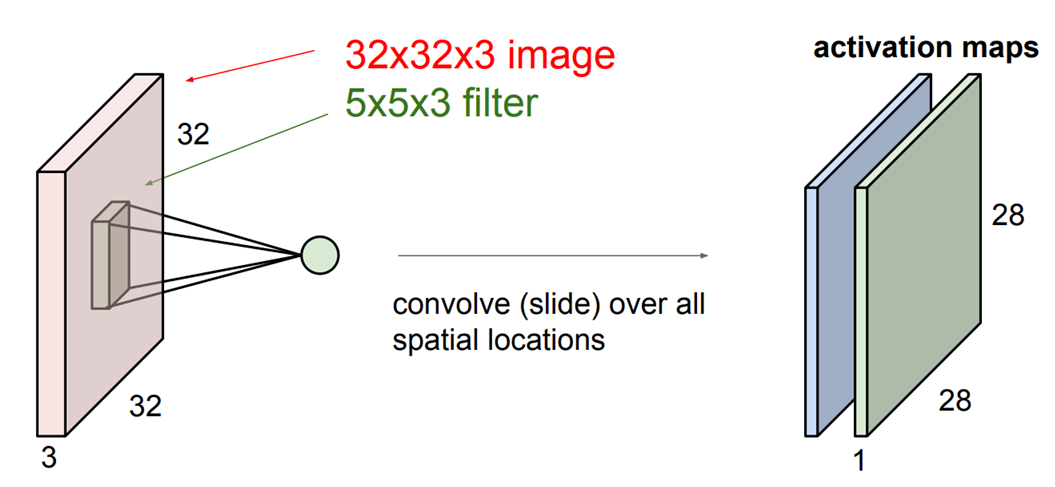
image 하나의 특징을 추출하는 과정이기에 filter와 image의 depth는 같습니다.
엄밀하게 여기서의 합성곱 연산은 신호처리 분야에서의 합성곱 연산과는 다릅니다. CNN에서의 합성곱연산은 합성곱의 의미적 요소만 가져온 것입니다.
*필터와 필터 크기에 맞는 이미지를 내적하는 것은 FC에서의 내적과정과 동일하다고 볼 수 있습니다.
Conv Layer를 Brain Neuron의 관점에서 살펴보겠습니다. 뉴런과 Conv Layer의 가장 큰 차이점은 뉴런은 Local Connectivity를 가지고 있다는 것입니다. Conv Layer처럼 슬라이딩을 하는 것이 아니라 특정 부분에만 연결되어 있습니다. 하나의 뉴런은 한 부분만 처리하고, 그런 뉴런들이 모여서 전체 이미지를 처리하는 것입니다. 그래서 여러개의 필터를 사용하여 해당 부분을 구현합니다. 각 필터가 하나의 뉴런과 비슷하게 작동하는 것입니다. 다양한 필터들이 다른 종류의 특징을 감지할 수 있도록 학습되기 때문입니다. 5x5 필터가 있다고 할 때, 한 뉴런의 “Receptive filed”가 5x5라고 이해할 수 있는 것입니다. “Receptive filed”란 한 뉴런이 한 번에 수용할 수 있는 영역을 의미합니다.
Conv Layer를 계층적으로 쌓아서 단순한 특징들을 뽑고, 그것을 또 조합해서 더 복잡한 특징으로 활용하는 식으로 활용합니다. 계층적 구조를 설계하고 역전파로 학습시키는 과정으로 필터를 학습시킵니다. 그림2는 각 그리드의 요소가 하나의 필터인데 이를 시각화 시킨 것입니다. 시각화 시킨 필터의 모습은 바로 이미지가 어떻게 생겨야 해당 필터의 활성을 최대화 시킬 수 있는지를 나타내는 것입니다. 이미지가 필터와 비슷하게 생겼으면 출력 값은 큰 값을 가지게 됩니다. 시각화는 역전파를 통해 해볼수 있습니다.(이를 자세히 다루는 내용은 추후 업데이트 하겠습니다.)
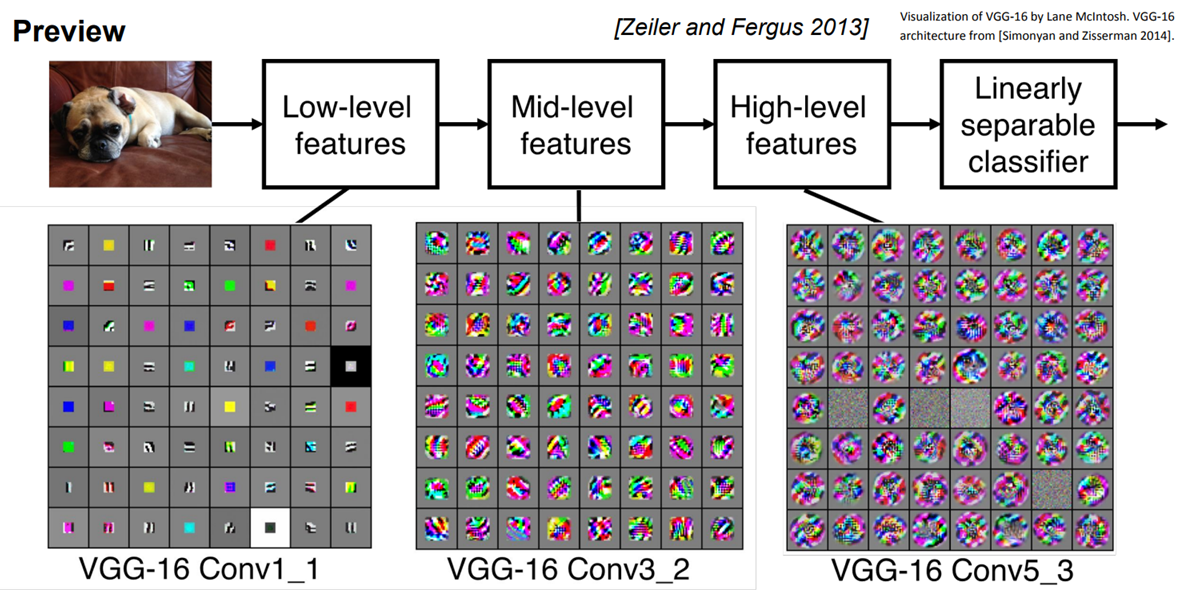
그림3은 이미지와 필터간 합성곱 연산의 activation 결과입니다. 빨간색 네모박스를 친 필터를 보면, 해당 필터는 edge를 찾고 있는 것입니다. 그리고 이 필터를 슬라이딩 시키면 이 필터와 비슷한 값들은 값이 커지게 됩니다. 따라서 각 activation은 이미지가 필터를 통과한 결과가 되며 이미지 중 어느 위치게서 이 필터가 크게 반응하는지를 보여줍니다. 우리가 이걸 Convolution이라고 부르는 이유는 위에 언급된 것과 같이 두 신호 사이에 cov를 하는 것과 유사하기 때문입니다.

Spatial Dimension에 대해서 알아보겠습니다. 이전에는 슬라이딩을 진행할 때 1칸씩 움직이는 것을 가정했습니다. 이렇게 움직이는 칸 수를 stride라고 합니다. 7x7 input과 3x3 filter를 가정할 때 stride는 1과 2가 될 수 있지만 3은 될 수 없습니다. 공간에 알맞게 슬라이딩이 진행되지 않기 때문입니다. 그림4를 보면서 찬찬히 생각해보시면 됩니다.
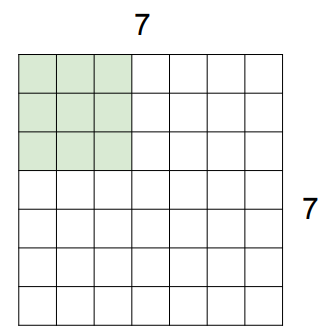
위의 과정을 수식적으로 나타내어 알맞은 stride값을 찾을 수 있습니다. N이 입력의 차원(그림3에서는 7), F가 필터 사이즈(그림3에서는 3)라고 한다면 Output size는 다음 식과 같이 정의될 수 있습니다. (N-F) / stride +1
이런식의 Conv layer는 층이 깊어질 수록 출력사이즈가 빠르게 줄어들기 때문에 padding을 사용하여 이를 해결할 수 있습니다. filter가 3x3일 때, zero padding을 그림3과 같이 적용할 수 있습니다. Output size를 정의하는 식에서 N이 N+2가 되었으므로, stride가 1일 때 (9-3) / 1+1로 output size가 input size와 같아지게 됩니다.
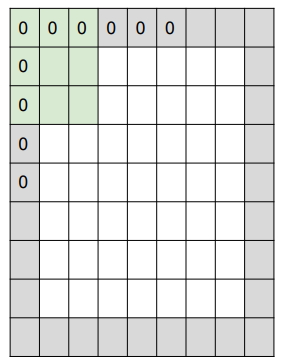
*다만 이러한 과정을 거치는 것은 “필요 없는 특징을 추가하는 것은 아닌지?”와 같은 의문을 남길 수 있습니다. 물론 모서리 부분에 약간의 artifact가 생길 수도 있습니다. 하지만 우리의 목적은 모서리 부분에서도 값을 얻어 size를 유지하는 것이고 zero padding 말고도 다른 방법들도 있습니다. 보통 필터는 3x3, 5x5, 7x7을 많이 쓰고 stride는 보통 1,2,3을 주로 사용합니다. 필터의 크기가 왜 홀수인지에 대해서는 다음 링크에 자세히 나와 있으니 참고하시길 바랍니다.
Question.
Input volume이 32x32x3이며 10개의 5x5 filters가 stride 1, pad2로 주어졌다고 할때, (1) Output size는 얼마인가? (2) 해당 layer에서 parameters의 개수는 얼마인가?
Answer.
(1) filter size가 5이고 pad가 2이기 때문에 size는 보존됩니다. 다음 식으로 유도됩니다. (32+22-5) / 1+1 그리고 필터가 10개이기 때문에 Output size는 32x32x10입니다.
(2) Depth와 bias를 고려하여 (555+1)10의 parameter를 가집니다.
만약 filter size가 1x1xdepth라면 어떨까요? 이런식이라면 공간적 정보를 사용하지 않는 특징이 있습니다.
stride를 크게 가져가면 어떨까요? 출력은 점점 작아지고, 이는 padding과 비슷합니다. 실제로 stride를 크게하는 것이 padding보다 모델의 성능이 좋다는 결과가 있습니다.
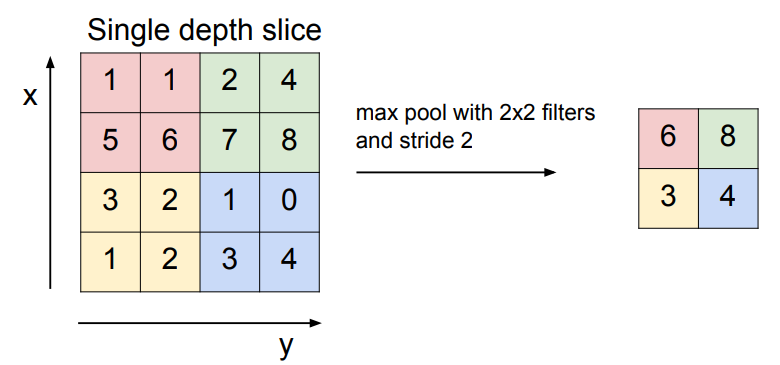
Pooling에 대해서 알아보겠습니다. Pooling은 결과를 더 작고 관리하게 쉽게해줍니다. 작아지면 parameter 수가 줄어드는 동시에 공간적 구조를 유지하기 때문입니다. 보통 Max pooling이 일반적으로 쓰입니다. 우리가 다루는 값들은 이 뉴런이 활성화되었는지를 나타내는 값들입니다. Max pooling은 그 지역이 어디든, 어떤 신호에 “얼마나” 그 필터가 활성화되었는지를 알려줍니다.(현재 필터와 뉴런을 혼용해서 쓰고 있습니다.)
9.3. CNN Backpropagation
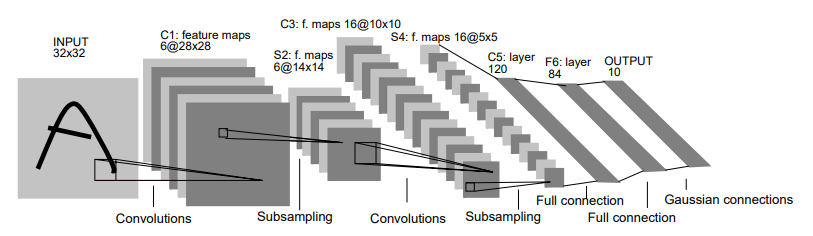
CNN구조를 적용한 LeNet의 전체 구조는 그림5와 같습니다. 전체적인 흐름을 한눈에 확인할 수 있습니다.
9.4. CNN Backpropagation
(추후 추가 예정)
9.5. CNN Test
https://pytorch.org/tutorials/beginner/blitz/cifar10_tutorial.html
9.6. Reference
[1] CS231n; Deep Learning for Computer Vision, Lecture5. CNN Architecture
[2] Deep Learning(Ian Goodfellow, Yoshua Dengio, Aaron Courvile)
[3] Gradient-Based Learning Applied to Document Recognition(Yann LeCunn, Leon Bottu, Yoshua Bengio, and Patrick Haffner, 1988)