Log Returns
Log returns
금융 분야에서 로그 수익률을 사용하는 이유는 보통 3가지 입니다. 이번 포스팅에서는 그 세가지 이유를 정리해보겠습니다. 우선 로그 수익률과 일반적인 수익률은 다음과 같이 정의 됩니다.
1. Normal returns
어떤 자산의 가격이 100원에서 130원이 되었다가 다시 100원으로 왔다고 가정해봅시다. 100원에서 130원이 될 때는 단순 수익률이 +30%이지만, 130원에서 100원이 될 때는 단순 수익률이 -30%가 아닌 -23%가 되는 문제가 발생합니다. 이는 연속시간에 대한 복리효과 때문입니다. 로그 수익률은 이를 보정하여 주가 변동 수익률의 합계가 최종 수익률과 같아지게 합니다.
2. Infinite support and Normality
1 | import yfinance as yf |
1 | from scipy.stats import lognorm |
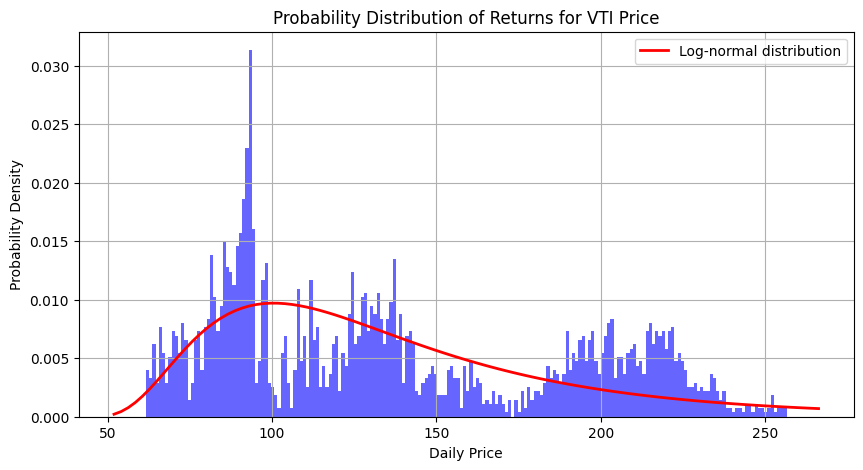
로그 수익률에 대한 일반적인 주장은, 가격이 로그 정규 분포인 경우 로그 수익률이 정규분포를 따른다는 것입니다. $zt=log(p_t)−log(p{t−1})$ 이므로, 로그 수익률은 두 정규 확률 변수의 합이기 때문입니다.(제 개인적인 생각은, $Pt$와 $P{t-1}$이 독립이 아니기 떄문에 말이 안되는 것 같습니다.)
그렇다면, 가격이 로그 정규분포를 따른다고 가정하는 것이 타당할까요? Vanguard Total Stock Market Index Fund ETF(VTI) 가격의 히스토 그램을 최적의 로그 정규분포와 함께 표시했습니다. 로그 정규 분포가 첫 번째 근사로 무리는 아니지만 데이터에 대한 좋은 모델은 아닌듯 합니다.1
2
3
4
5
6
7
8
9
10import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(10, 6))
sns.kdeplot(df['Return'].dropna(), bw_adjust=0.5, color='b')
plt.title('Probability Distribution of Simple Returns for VTI')
plt.xlabel('Daily Return')
plt.ylabel('Probability Density')
plt.grid(True)
plt.show()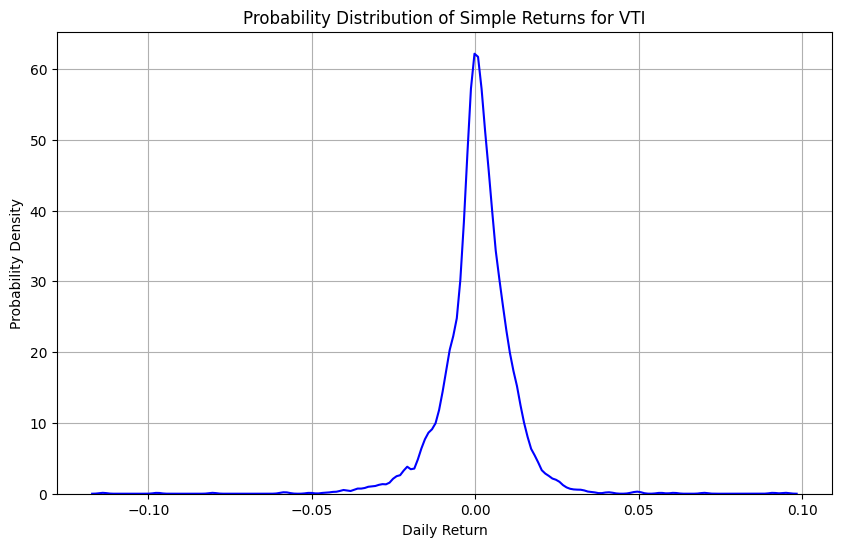
1
2
3
4
5
6
7
8
9
10import matplotlib.pyplot as plt
import seaborn as sns # Seaborn 라이브러리를 사용하여 KDE plot을 그립니다.
plt.figure(figsize=(10, 6))
sns.kdeplot(df['Log_Return'].dropna(), bw_adjust=0.5, color='g')
plt.title('Probability Distribution of Log Returns for VTI')
plt.xlabel('Daily Return')
plt.ylabel('Probability Density')
plt.grid(True)
plt.show()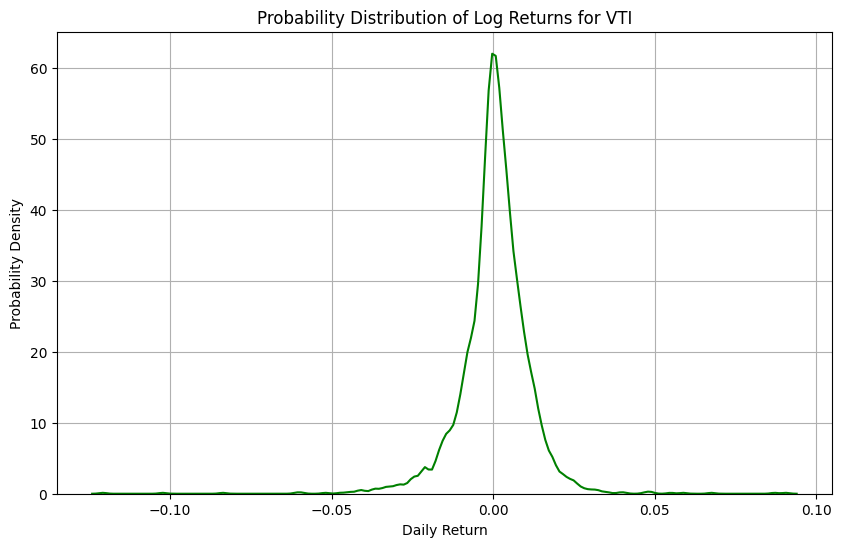
1
2
3
4
5
6
7
8
9
10
11plt.figure(figsize=(10, 8))
(result, _) = stats.probplot(df['Log_Return'].dropna(), dist="norm")
plt.plot(result[0], result[1], 's', color='green',alpha=0.9, label='Log_Return')
stats.probplot(df['Return'].dropna(), dist="norm", plot=plt)
plt.title('Q-Q Plot of Log Returns for AAPL')
plt.ylabel('Ordered Values')
plt.xlabel('Theoretical Quantiles')
plt.legend()
plt.grid(True)
plt.show()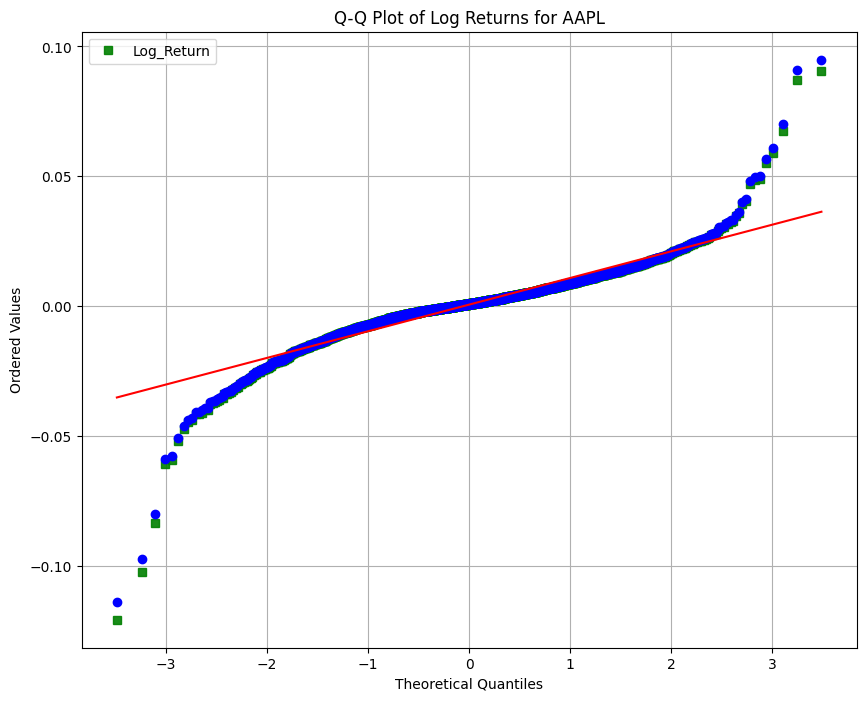
수익률의 하한은 -1.0입니다. 하지만, 로그 수익률은 무한한 범위를 가집니다. 그리고 로그함수는 큰 양의 값을 누르고 작은 음의 값을 키우므로, 단순 수익률보다 로그 수익률이 더 대칭적입니다. 실제로, 위 그림과 같이 작동하는 모습을 볼 수 있습니다. 단순 수익률과 로그 수익률 모두 정규분포보다 꼬리가 더 두껍습니다. 이론적으로 아래 그림과 같이 단순 수익률은 음의 왜도와 3이상의 첨도를 가져, 로그변환을 해주면 정규분포 모양으로 가까워 질 것을 기대할 수 있습니다. 하지만, 실제로는 위 그림와 같이 더 대칭적이지 않게 되는 모습도 보입니다.
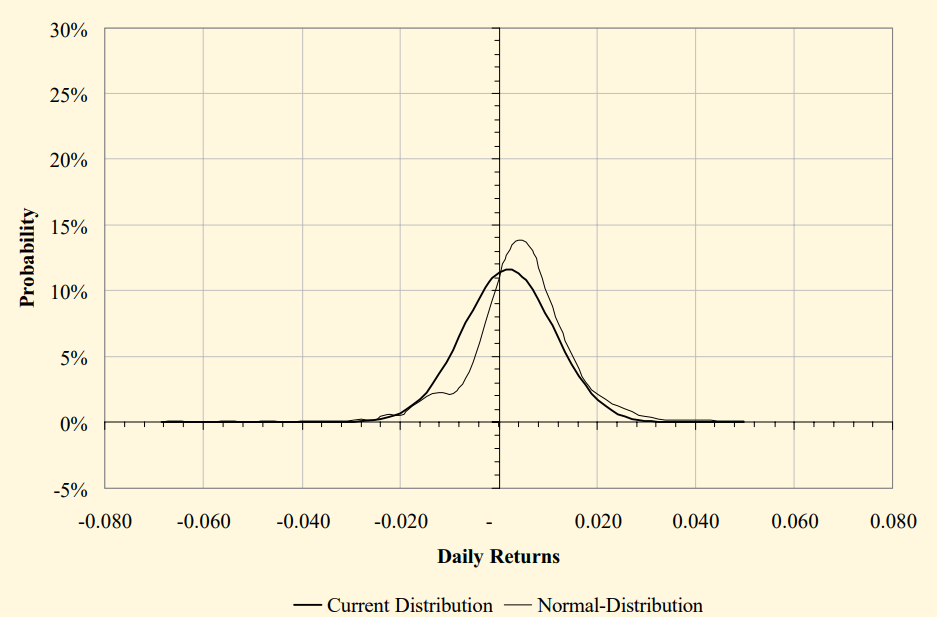
3. The Relationship Between Log Returns and Simple Returns
연속 복리 수익의 계산은 다음과 같습니다. 로그 수익률은 한기간 동안의 연속 복리 수익률($e^r$)이 단순 수익률일 때, r을 구하는 것입니다.
4. Approximations
로그 수익률을 쓰는 마지막 이유는 수학적 특성 외에도 원시 수익률과 유사한 경우가 많기 때문입니다. $x$가 0근처일때, 다음을 만족합니다. $log(1+x)≈x$ 그리고 수익률은 보통 0근처입니다. 실제로 $y = ln(x+1)$의 first-order taylor sereis는 $y = x$입니다(증명 생략).
Reference
[1] https://gregorygundersen.com/blog/2022/02/06/log-returns/
[2] MTI OPENCOUSE - Invseting(2008)