MVO 이것저것 실험

해당 게시물은 평균 분석 최적화(MVO) 공부하면서 제가 이것저것 실험해본 것들입니다.

평균 분산 최적화와 제약조건

단일 기간 분석에서, 다음과 같이 최적화 문제를 정의하겠습니다.

m개의 위험자산: i = 1, 2, …, m

단일 기간 수익률: m-variate random vector

$$\mathbf{R} = \begin{bmatrix} R_1 \\ R_2 \\ \vdots \\ R_m \end{bmatrix}$$

평균과 분산/수익률의 공분산:

$$\mathbb{E}[\mathbf{R}] = \boldsymbol{\alpha} = \begin{bmatrix} \alpha_1 \\ \vdots \\ \alpha_m \end{bmatrix}, \quad \text{Cov}[\mathbf{R}] = \Sigma = \begin{bmatrix} \Sigma_{1,1} & \cdots & \Sigma_{1,m} \\ \vdots & \ddots & \vdots \\ \Sigma_{m,1} & \cdots & \Sigma_{m,m} \end{bmatrix}$$

포트폴리오: m-vector of weights indicating the fraction of portfolio wealth held in each asset

$$\mathbf{w} = (w_1, \ldots, w_m) \text{ with } \sum_{i=1}^{m} w_i = 1$$

포트폴리오 수익률:

$$R_w = \mathbf{w}'\mathbf{R}$$

는 다음과 같은 확률 변수를 가집니다:

$$\alpha_w = \mathbb{E}[R_w] = \mathbf{w}'\boldsymbol{\alpha}$$ $$\sigma^2 = \text{var}[R_w] = \mathbf{w}'\Sigma\mathbf{w}$$

포트폴리오의 평균-분산 쌍인 $(\alpha{\mathbf{w}}, \sigma{\mathbf{w}}^2)$을 사용하여 다양한 포트폴리오 $\mathbf{w}$를 평가합니다. 이때 선호되는 것은:

• 더 높은 기대 수익률 $\alpha_{\mathbf{w}}$
• 더 낮은 분산 $\text{var}_{\mathbf{w}}$

위험 최소화: 주어진 목표 평균 수익률 $\alpha_0$에 대해, 다음 조건을 만족시키는 포트폴리오 $\mathbf{w}$를 선택합니다.
Minimize:$\mathbf{w}’\Sigma\mathbf{w}$
Subject to:

$$\mathbf{w}' \mathbf{1}_m = 1$$ $$\mathbf{w}' \boldsymbol{\alpha} = \alpha_0$$

평균분산 최적화의 기하적 해석(2개 자산)

	KODEX KOSPI (226490.KS)	KIM ACE KRX Physical Gold ETF(411060.KS)
기대 수익률(평균 일일 로그수익률)	0.000825	0.000544
변동성(표준편차)	0.009675	0.007906
샤프비율(무위험 수익률 = 0)	0.08524	0.068851
공분산 행렬	0.000094	-0.000018
	-0.000018	0.000063

표1: 포트폴리오 편입 자산 정보 그림1: 2개 자산의 누적 수익률**

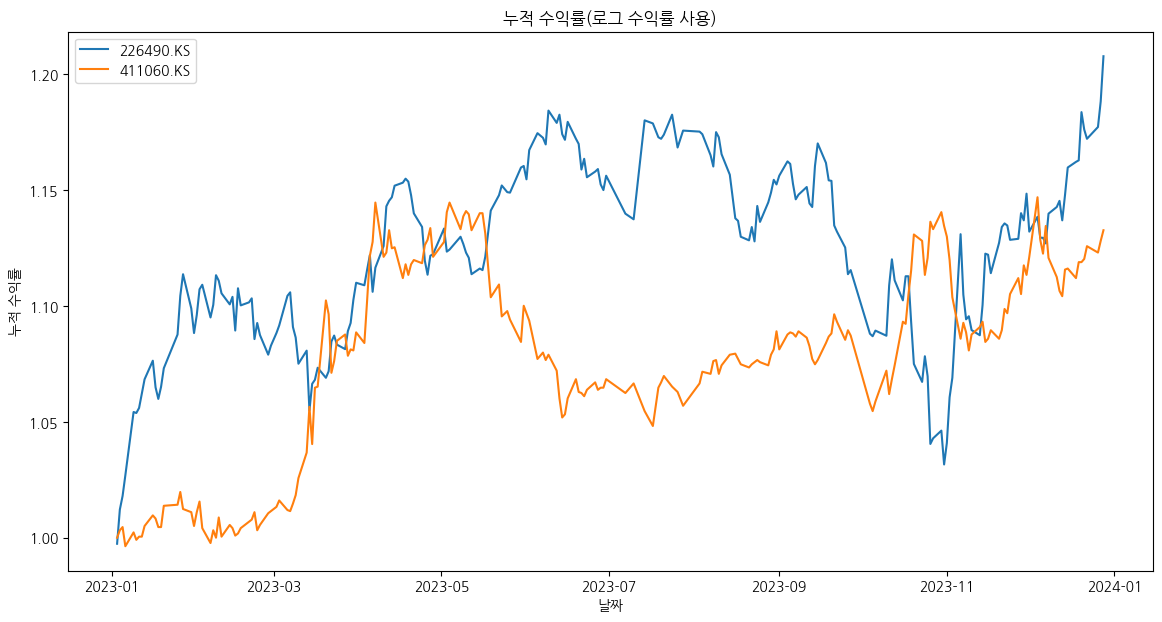
위에서 설명한 평균분산 최적화 문제를 2개의 자산에 대해 적용하겠습니다. 대한민국 주식시장(유가증권시장)에 포함된 전 종목으로 구성된 지수 수익률을 추적하는 ‘KODEX 코스피(226490.KS)와 금 현물 가격을 추종하는 ‘KIM ACE KRX Physical Gold ETF(411060.KS)’를 자산으로 결정하였습니다. KOSPI Yahoo Finance에서 제공하는 2023-01-01 부터 2023-12-31까지의 수정주가 데이터를 사용하였습니다. 표1은 포트폴리오로 편입할 두 자산의 정보, 그림1은 2개 자산의 누적 수익률을 나타냅니다.

그림2: 무제약조건하의 목적함수 그래프

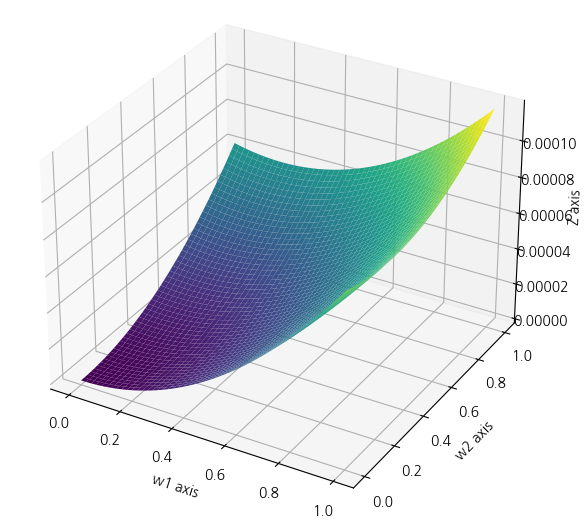
우선 무제약조건하의 목적함수 $\mathbf{w}’\Sigma\mathbf{w}$ 를 그림2와 같이 나타냅니다. Z축은 포트폴리오의 변동성을 나타냅니다.

그림3: 첫번째 제약조건하의 목적함수 그래프

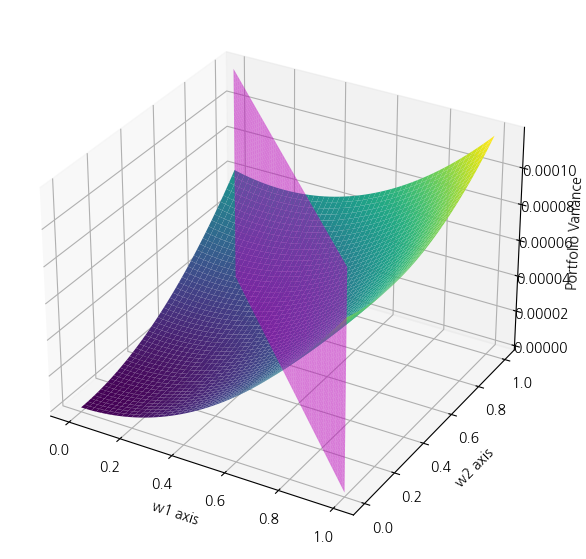
그 후, 첫번째 제약조건을 그림3과 같이 나타냅니다. 곡면과 평면이 만나는 곡선위에서 최적점이 결정됩니다.

그림4: 두 제약조건하의 목적함수 그래프1

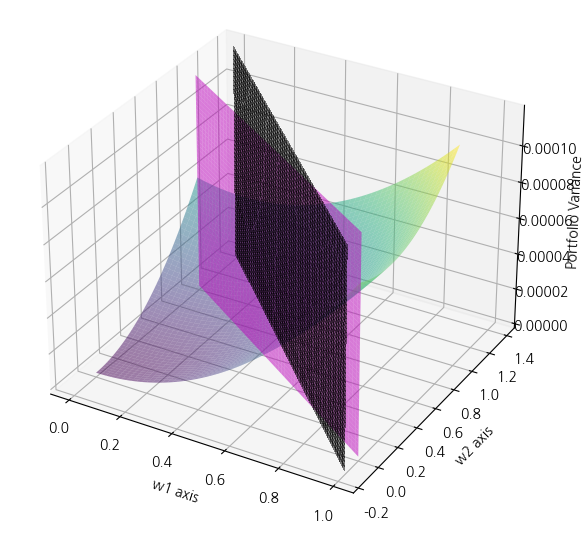
두번째 제약조건을 추가해 그림4와 같이 나타냅니다. 검정 평면 오른쪽으로 최적점이 결정됩니다.

그림5: 두 제약조건하의 목적함수 그래프2

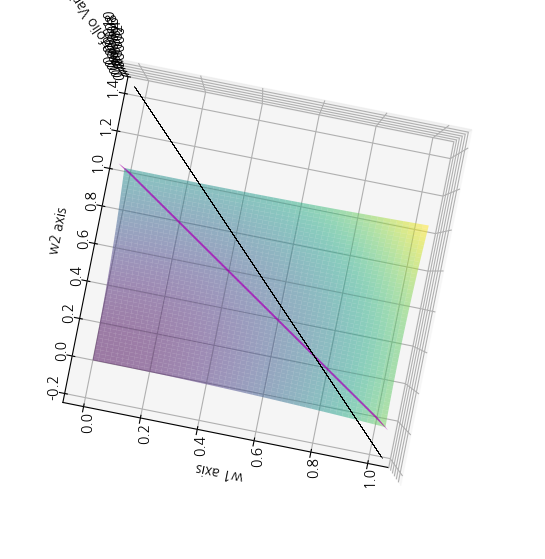
그림4를 위에서 내려다보면 그림5와 같은 모양이 됩니다. 검정 선 오른쪽공간과 보라색 선의 교집합에서 최적점이 결정됩니다.

그림6: 두 제약조건하의 목적함수 그래프3

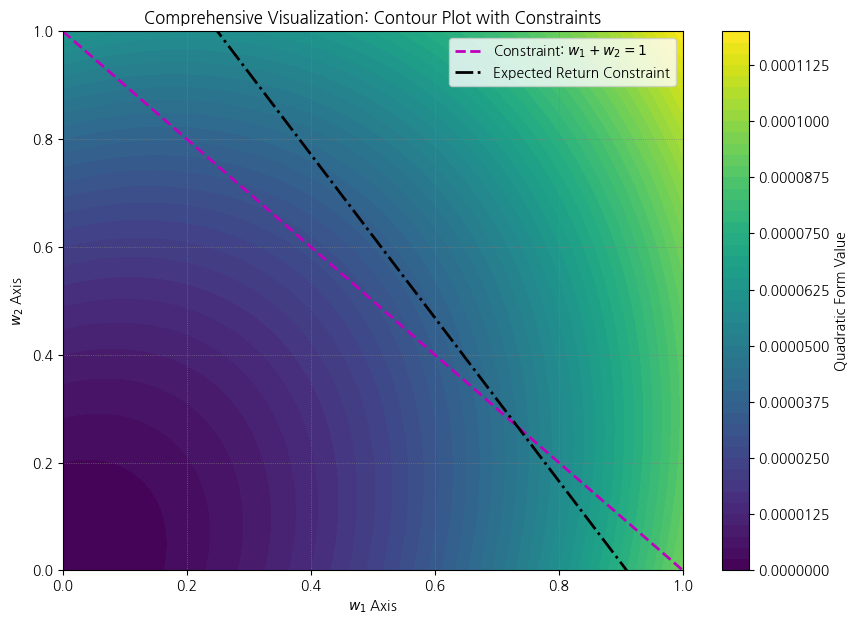
그림5를 w1과 w2를 축으로 표기하면 그림6과 같습니다. 이떄, 평면위의 한점은 가중치 벡터가 됩니다.

---

이번에는 2개 자산에서 공분산 행렬의 변화에 따른 그래프의 모양을 보고자 합니다.

그림7: 두 자산이 양의 상관관계일떄 상관계수에 따른 곡률변화 그림8: 두 자산이 음의 상관관계일떄 상관계수에 따른 곡률변화

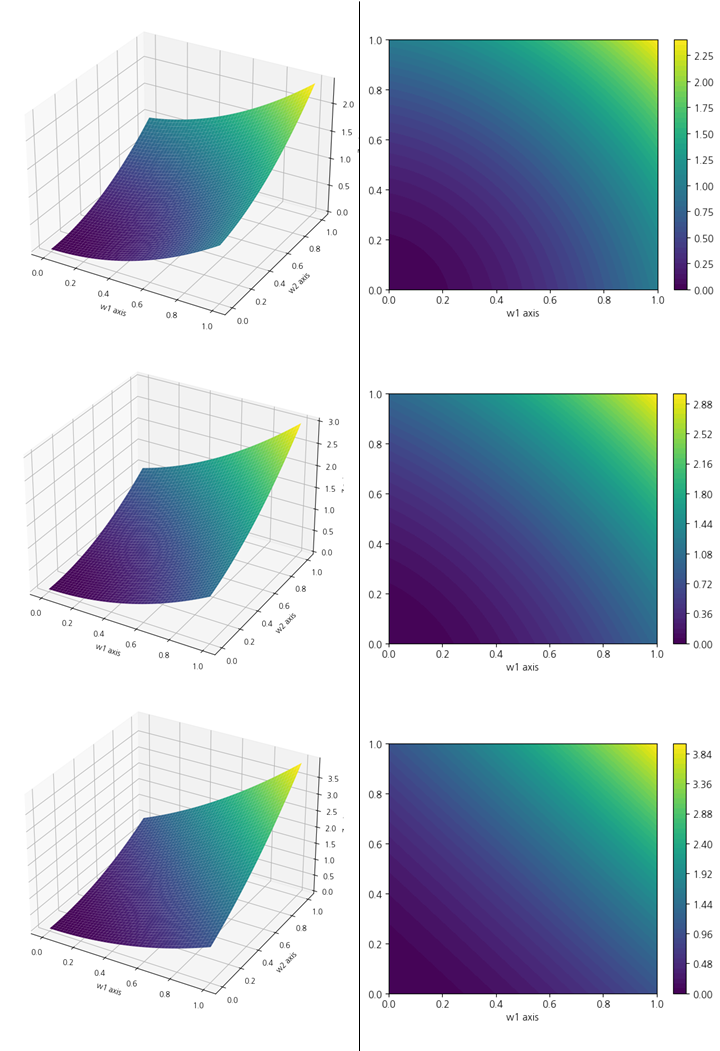
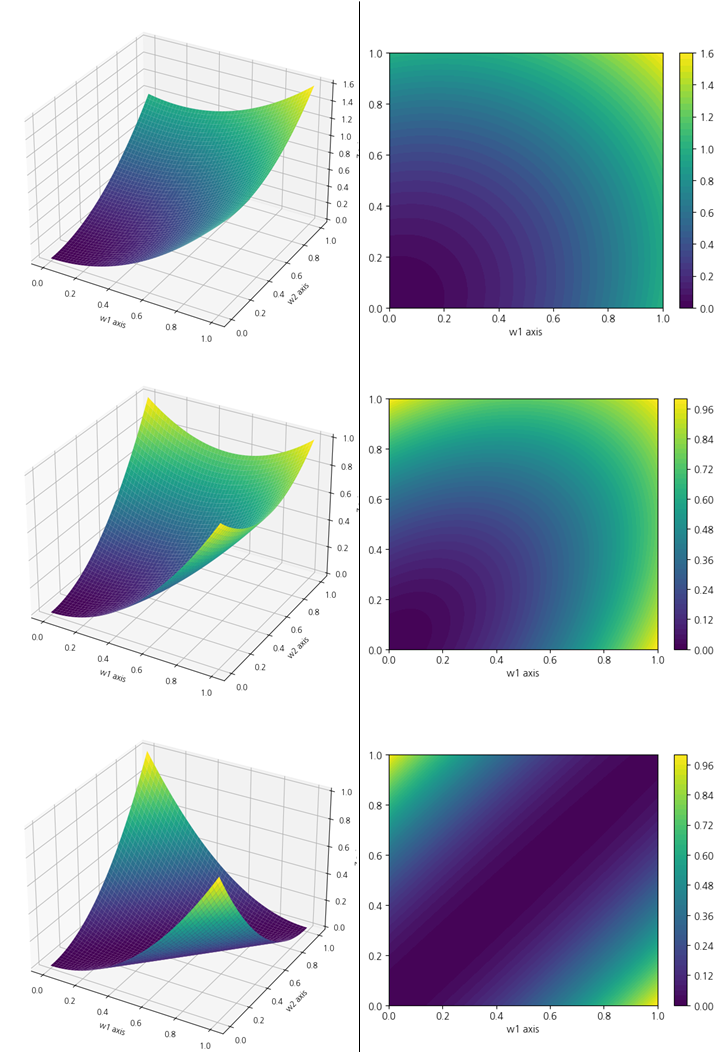
그림7은 두 자산간의 상관관계가 양(+)이고, 그 절댓값을 점점 키우는 경우의 모습입니다. 그림8은 두 자산간의 상관관계가 양(+)이고, 그 절댓값을 점점 키우는 경우의 모습입니다. 자산간의 상관관계에 따라 곡면의 곡률 그리고 상한 및 하한이 변하는 모습을 볼 수 있습니다. 이는 공분산 행렬의 추정에 있어 강건하게 추정하지 않으면 포트폴리오의 위험을 과대/과소평가 할 수 있음을 의미합니다.

평균분산 최적화의 기하적 해석(3개 자산)

3개 자산에서 코너해가 발생하는 경우를 시각화 해보도록 하겠습니다. 그림9~11은 각 축이 w1, w2, w3이며, 삼각형 모양을 가진 2차원 공간은 w1 + w2 + w3 = 1의 제약조건을 만족하는 공간입니다.

그림9: 3개 자산에서 가중치 행렬의 변화에 따른 포트폴리오 변동성 시각화1 $\Sigma = \begin{bmatrix} 1 & 0.2 & 0.1 \\ 0.2 & 1 & 0.1 \\ 0.1 & 0.1 & 1 \\ \end{bmatrix}$ 그림10: 3개 자산에서 가중치 행렬의 변화에 따른 포트폴리오 변동성 시각화2 $\Sigma = \begin{bmatrix} 1 & 0.9 & 0.1 \\ 0.9 & 1 & -0.1 \\ 0.1 & -0.1 & 1 \\ \end{bmatrix}$

그림11: 3개 자산에서 가중치 행렬의 변화에 따른 포트폴리오 변동성 시각화3

$\Sigma = \begin{bmatrix} 1 & -0.9 & 0.1 \\ -0.9 & 1 & 0.1 \\ 0.1 & 0.1 & 1 \\ \end{bmatrix}$


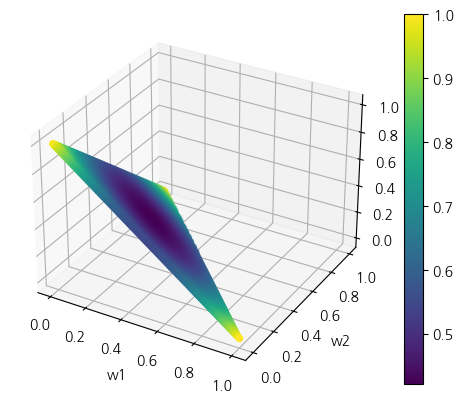
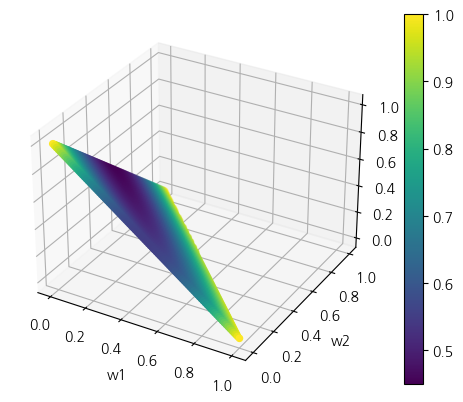
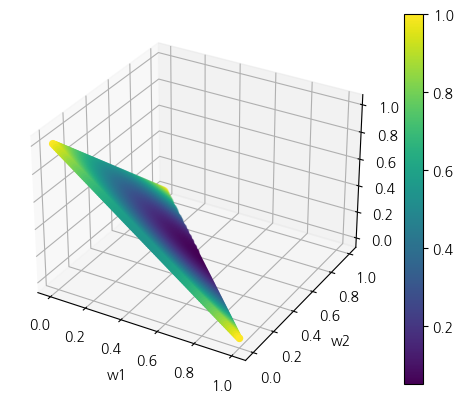
목표 수익률의 등식/부등식 제약조건을 어떻게 잡느냐에 따라 달라지겠지만, 최적점이 있을 확률이 높은 부분 즉, 어두운 부분이 실제로 코너로 이동하는 것을 확인할 수 있습니다. 이는 공분산 행렬의 추정에 있어 강건하게 추정하지 않으면 비효율적인 자산배분이나 코너해를 가질 수 있음을 의미합니다.

Reference

[1] Portfolio Optimization: a comparison among Markowitz, Black - Litterman and
Robust Optimization approach(LUISS, 2019/2020)