Numerical Integration [1]

작성일 Edited on In , Disqus:

수치적분관련 간단한 방법들의 시뮬레이션을 진행해봄.
기본 내용은 James Stewart의 Calculus 참고했고, 더 자세한 내용은 Unified Proofs of the Error Estimates for the Midepoint, Trapezoidal, and Simpson’s Ruls 참고하였음.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
import numpy as np
from tabulate import tabulate

# 정의역 설정
a = 0
b = np.pi

k = 6  # 소수점 k번째 까지 잘라서 출력

# Simpson's Rule 떄문에 n을 홀수로 설정해야됨.
n_values = [5, 11, 21, 51, 101]
approximations = []
errors = []

for n in n_values:
    h = (b - a) / (n - 1) 
    x = np.linspace(a, b, n)
    f = np.sin(x)

    # Left Riemann sum
    I_riemannL = h * sum(f[:n-1])
    err_riemannL = 2 - I_riemannL

    # Right Riemann sum
    I_riemannR = h * sum(f[1:])
    err_riemannR = 2 - I_riemannR

    # Midpoint Rule
    I_mid = h * sum(np.sin((x[:n-1] + x[1:]) / 2))
    err_mid = 2 - I_mid

    # Trapezoidal Rule
    I_trap = (h / 2) * (f[0] + 2 * sum(f[1:n-1]) + f[n-1])
    err_trap = 2 - I_trap

    # Simpson's Rule
    I_simp = (h / 3) * (f[0] + 2 * sum(f[2:n-2:2]) + 4 * sum(f[1:n-1:2]) + f[n-1])
    err_simp = 2 - I_simp

    # 근사값이랑 에러 저장
    approximations.append([
        n, round(I_riemannL, k), round(I_riemannR, k),
        round(I_mid, k), round(I_trap, k), round(I_simp, k)
    ])
    errors.append([
        n, round(err_riemannL, k), round(err_riemannR, k),
        round(err_mid, k), round(err_trap, k), round(err_simp, k)
    ])

# 표 헤더 저장
approx_headers = [
    "n", "L Riemann", "R Riemann", "Midpoint", "Trapezoid", "Simpson"
]
error_headers = [
    "n", "L Error", "R Error", "Mid Error", "Trap Error", "Simp Error"
]

# 표 출력
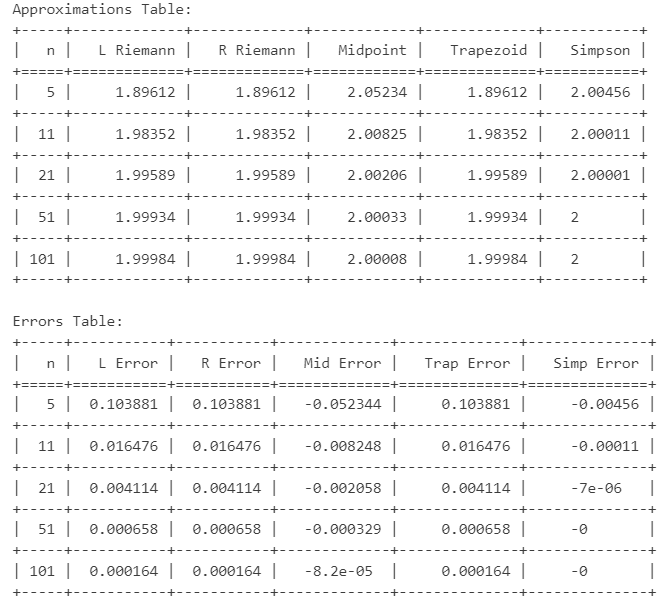
print("Approximations Table:")
print(tabulate(approximations, headers=approx_headers, tablefmt="grid"))

print("\nErrors Table:")
print(tabulate(errors, headers=error_headers, tablefmt="grid"))